При помощи геометрической схемы, которая и именуется круги Эйлера, можно наглядно установить связи между понятиями. Кроме того, наглядно видно, какое отношение существует между частью множества и им самим.
Достоинство кругов Эйлера в том, что они помогают упростить рассуждения и получить наглядный ответ. Сам Леонард Эйлер, придумавший данный метод, так и объяснял его значимость. Несмотря на то, что учёный предложил свой способ 3 столетия назад, он и сегодня актуален, так как помогает наглядно увидеть задачу и способ её решения.
Круги могут пересекаться или не пересекаться, а также один круг может быть вложен в другой.
Практическое значения метода в том, что он помогает решать сложные задачи, когда объединяются или пересекаются множества. Благодаря данному методу развиваются такие умения, как:
- анализ, когда ребята умеют выделять главные и второстепенные признаки представленных предметов;
- синтез, когда учатся объединять предметы по какому-либо признаку;
- классификация, сравнение, умение достраивать недостающие элементы, установление причинно-следственных связей.
Применяются круги Эйлера для решения простейших задач уже в детском саду. Ребята учатся мыслить логически, а также применяют простейшие математические знания. В дальнейшем приобретённые навыки понадобятся детям для подготовки к школе и решения более сложных задач.
Примеры задач для детей 2-3 лет
Знакомства с кругами Эйлера можно начинать в раннем возрасте. Конечно, предложенные задания будут элементарными.
Например, можно попросить малыша положить в круг (его роль выполняет обыкновенный обруч) мяч. Второй мяч надо положить вне круга. После этого два обруча надо наложить один на второй и предложить ребёнку положить мяч так, чтобы он оказался сразу в двух кругах.
Усвоим элементарные понятия, можно приступать к более сложному – выполнению некоторых задач, которые в состоянии решить ребёнок. Конечно, подбирать задания необходимо в соответствии с возрастом и умениями конкретного ребёнка.
Примеры задач, которые помогут понять детям 4-5 лет что значит круги Эйлера
Ребятам в таком возрасте под силу решить следующие задачи. Начинаются они простого уровня сложности идут по возрастанию.

Простой уровень
Найти предмет по двум свойствам
Дети видят 3 карточки, где изображены кубик Рубика, пирамидка и мячик. В двух кругах задано условие: надо выбрать предмет квадратной формы и разноцветный. Подходит только кубик.
Найти животное
Задача аналогична предыдущей. Дети должны выбрать зелёное маленькое животное из предлагаемых. Это заяц, лягушка и хомяк. Параметры заданы снова в кругах. Под описание подходит только лягушка.
Найти фрукты
И это задание построено по аналогии с предыдущим. Из фруктов (предложена клубника, лимон и жёлтая груша) необходимо выбрать жёлтый, но при этом сладкий. Ответ очевиден – это груша.
Средний уровень
Больше множеств
Детям предлагается найти предмет из трёх предложенных (солнце, фонарь и цыплёнок), который описан в кругах как яркий, тёплый и жёлтый. Здесь надо применить сразу 3 характеристики. И подходят они солнцу.
По аналогии можно предложить дать ответ относительно одежды или любых других предметов.
Выбрать круг с неправильной характеристикой
Можно пойти от обратного и попросить найти описание, которое совсем не подходит к предмету. Например, предлагается изображение чипсов, а затем их свойства: полезные, вкусные, картофельные, хрустящие. Слово «полезные» окажется лишним.

Разложить предметы в два круга
Нескольким детям предлагается разложить предметы, лежащие на столе. В одном кругу должны оказаться кукла, мячик, пирамидка, кораблик, самолётик и машинка. К слову, мячик, машинка и кукла жёлтого цвета.
Сначала ребятам предлагается положить транспорт в один круг, а игрушки в другой. Обычно такое задание не вызывает труда и выполняется быстро.
Задание усложняется. Детям предлагается положить в один круг предметы, относящиеся к транспорту, а во второй поместить предметы жёлтого цвета. Тогда и возникнет вопрос: куда надо поместить машинку? Одна и транспорт, и в то же время имеет жёлтый цвет.
В результате разгоревшейся дискуссии дети приходят к выводу: машинка должна быть сразу в двух кругах. Значит, их надо наложить один на другой так, чтобы получилось общее.
Задача про друзей
Ребятам предлагается следующая задача. У Васи несколько друзей. 5 из них любят заниматься спортом, а 4 предпочитают читать книги. 2 друга и читают, и занимаются спортом.
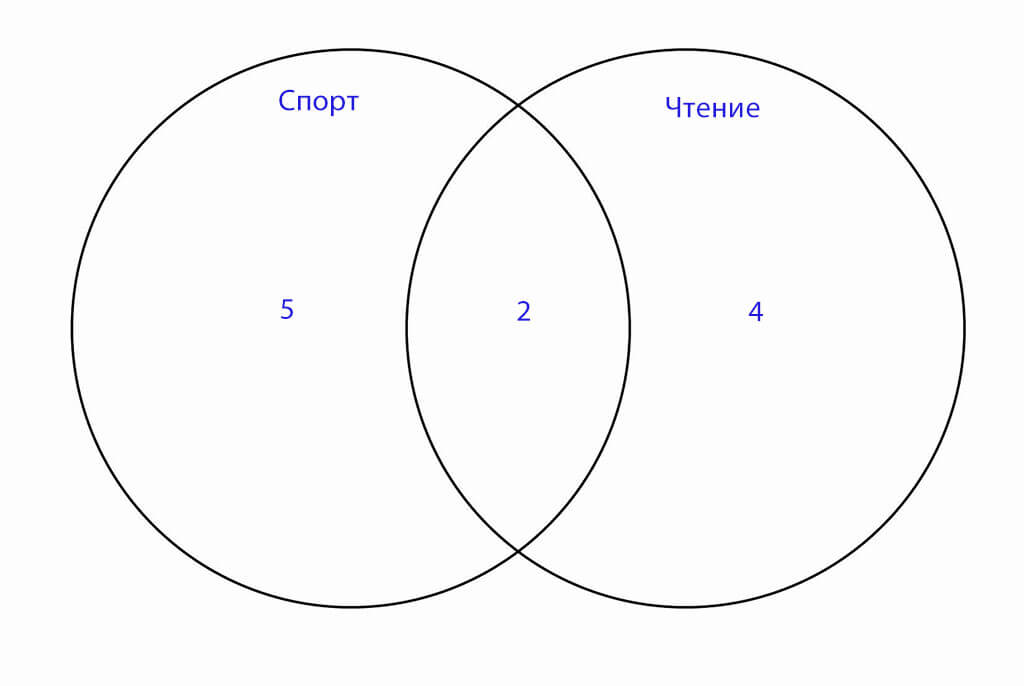
Дети в один круг вписывают цифру 5, во второй – 4, а на пересечении кругов оказывается 2. Таким образом, наглядно видно, что у Васи всего 11 друзей.
Примеры задач для детей школьного возраста
Школьники быстро усваивают разницу между геометрическими фигурами при помощи кругов Эйлера.
Задача 1
Дети решают задачу. Бассейн посещают 45 школьников. Из них 35 постоянно ходят в школьный бассейн, а 20 – регулярно в городской. Предлагается ответить на вопросы:
Сколько школьников:
- Посещают как школьный, так и городской бассейн?
- Не ходят в городской бассейн?
- Не ходят в школьный бассейн?
- Посещают только школьный бассейн?
- Посещают только городской бассейн?
Решение.
Чтобы определить, сколько школьников посещают оба бассейна, необходимо выполнить следующее действие: (35 + 20) – 45 = 10
В городской бассейн не ходят 25 учащихся, так как 45 – 20 = 25
В школьный бассейн не ходят 10 учащихся, так как 45 – 35 = 10
Только в городской бассейн ходят 10 школьников: 45 – 35 =10
Только в школьный бассейн ходят 15 школьников: 45 – 20 = 15
Задача 2
Предлагается ещё одна задача. Надо узнать, количество рабочих, которые строят магазин и фабрику, если известно, что всего рабочих 30, из них 16 – заняты на строительстве магазина, а 20 – на строительстве фабрики.
Для решения сначала надо узнать, сколько человек строят только магазин. Для этого от 30 необходимо отнять 16. В результате получится 14. Затем выполняется следующее действие: 20- 14 = 6. Получается, что 6 рабочих трудятся сразу на двух объектах.
Круги Эйлера помогают наглядно увидеть условие задачи, а также найти способ решения. В этом и заключается практическая ценность данного метода.













